参加メモ:第1回「ゼロから作るDeep Learning」読書会 in 銀座
イベント概要
- 第1回「ゼロから作るDeep Learning」読書会 in 銀座
- 主催 : 株式会社メイプルシステムズ (勉強会初開催らしい)
- 日時:2017/01/25(水) 19:30 〜 21:30
- 会場:メイプルシステムズオフィス
まえがき
- ディープラーニングを作るためには、多くの試練がある
- この本は、車の運転で例えるなら、車の教習本ではなく、車の原理について理解してもらうことを主眼としている
1. Pythonの概要
1.1 Pythonとは
- 高い可読性&&ハイパフォーマンスなので、機械学習やデータサイエンスでよく使われている
- NumPy(なんぱい), SciPy(さいぱい)など数値計算や統計処理の優れたライブラリが整備されている
- ディープラーニングのフレームワーク(CaffeやTensorFlow、ChainerやTheano)はCoreなところはCとかマシン語にコンパイルできる言語だけど、Pythonから使えるinterfarceが用意されている
1.2 Pythonのインストール
- とりあえずAnacondaディストリビューション入れよう
- ゼロから作るとは言ってるけどNumPy(数値計算のためのライブラリ)とMatplotlib(グラフ描画のためのライブラリ)は使う
- Anacondaディストリビューションを使うとNumPy, Matplotlibが含まれているのでおすすめ。
- 数値を見やすくするのがこの分野では大事
1.3 Python インタプリタ
- いわゆるREPL環境 (Read-Eval-Print Loop)
$ python$ ipython$ jupyter notebook←おすすめ:WEBブラウザから使える対話環境
1.4 Python スクリプトファイル
- もちろんREPLだけじゃなくて、普通のプログラムと同じでファイルに書いて実行もできる
1.5 NumPy
import numpy as np # ライブラリを使うためにnpという名前でインポートする
- コアな部分をC言語/C++で実装されていて呼び出すところだけがPythonで実行している数値計算ライブラリ
- 生のPythonは命令を一つ一つインタープリタが解釈するので、大量のデータをさばくのには向かない
足し算
x = np.array([1.0, 2.0, 3.0]) y = np.array([2.0, 4.0, 6.0]) x+y
array([3., 6., 9.])
掛け算
要素ごとの計算と解釈される
x = np.array([1.0, 2.0, 3.0]) y = np.array([2.0, 4.0, 6.0]) x*y
array([2., 8., 18.])
N次元配列
- 多次元の配列もいい感じに計算してくれる
- arrayを入れ子にすることで行列も表現できる
行列の足し算/引き算
- 成分ごとの足し算/引き算
行列の掛け算/割り算
- 成分ごとの掛け算/割り算。行列の積とは違うが、成分ごとの掛け算のほうがよく使う。
- 行列の積と使う場合はdot()関数を利用する
1.6 Matplotlib
sin関数
%matplotlib inline # ブラウザ内で表示するために書いておく import matplotlib.pyplot as plt x=np.arrange(0, 6, 0.1) # 0から6を0.1刻みで増やす y = np.sin(x) plt.plot(x, y) plt.show()
画像の表示
import matplotlib.pyplot as plt
from matplotlib.image import imread
img = imread('lena.png') # 画像の読み込み(適切なパスを設定する!) plt.imshow(img)
plt.show()
1章まとめ
- Python はシンプルで覚えやすいプログラミング言語である。
- Python はオープンソースで自由に使うことができる。
- 本書のディープラーニングの実装では Python 3 系を利用する。
- 外部ライブラリとして NumPy と Matplotlib を利用する。
- Python の実行モードには「インタプリタ」と「スクリプトファイル」の2 つのモードがある。
- Python では関数やクラスといったモジュールとして実装をまとめることができる。
- NumPy には多次元配列を操作するための便利なメソッドが数多くある。
2. パーセプトロン
2.1. パーセプトロンとは
- 脳の神経回路を模倣したのがニューラルネットワークなので、パーセプトロンはニューロンっていう(シナプスがニューロンに電気刺激を送られて、シナプスが反応して次につながっているシナプスに連鎖反応で脳はできている)
- perceptron←perception(知覚、認識)から取ってるっぽい
- 複数の信号を入力として受取、ひとつの信号を出力するプログラム。
- 信号は0/1のみ
- あるニューロンへの信号の総和がしきい値(θ)を超えると発火(=出力)する。
- しきい値(θ)や重み(w)もパーセプトロンの一部なので、これらを変えることでパーセプトロンの動きが色々変化する
2.2 単純な論理回路
ANDノード, NANDノード, ORノードをパーセプトロンで表現してみよう
AND回路
y= 0(w1x1+w2x2<=θ) 1(w1x1+w2x2>θ)
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1 * w1 + x2 * w2
if tmp<= theta:
return 0
elif tmp>theta:
return 1
print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))
0 0 0 1
しきい値ではなくバイアス(-b)に置き換える
y= 0(b+w1x1+w2x2<=0) 1(b+w1x1+w2x2>0)
- θを左辺に移行できるので、右辺がいつも0になるので整理された感じになる
- 重みとバイアスを変えるだけで他のところは変えずにいろんな回路ができる
- 基本のパーセプトロンは使いまわせる。その重みを変えるだけで調整ができる
def AND(x1, x2):
w1, w2, b = 0.5, 0.5, -0.7
tmp = x1 * w1 + x2 * w2 + b
if tmp<= 0:
return 0
elif tmp>0:
return 1
print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))
NAND回路
def NAND(x1, x2):
w1, w2, b = 0.5, 0.5, -0.7 # ここしか変えてない
x = np.array([x1, x2])
w = np.array([w1, w2])
tmp = np.sum(w * x) + b
if tmp<= 0:
return 0
elif tmp>0:
return 1
print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))
OR回路
def OR(x1, x2):
w1, w2, b = 0.5, 0.5, -0.2 # ここしか変えてない
x = np.array([x1, x2])
w = np.array([w1, w2])
tmp = np.sum(w * x) + b
if tmp<= 0:
return 0
elif tmp>0:
return 1
print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))
パーセプトロンの限界
多層パーセプトロン
- パーセプトロンを重ねると実現できる
def XOR(x1, x2):
# 重み、バイアスは一旦忘れる
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
NANDからコンピュータへ
- 多層のパーセプトロンを組み合わせればコンピュータも表現できる
- ここでいうコンピュータはなんだろう :thinking_face:
まとめ
- パーセプトロンは入出力を備えたアルゴリズムである。ある入力を与えたら、決まった値が出力される。
- パーセプトロンでは、「重み」と「バイアス」をパラメータとして設定する。
- パーセプトロンを用いれば、AND や OR ゲートなどの論理回路を表現で きる。
- XOR ゲートは単層のパーセプトロンでは表現できない。
- 2 層のパーセプトロンを用いれば、XOR ゲートを表現することができる。
- 単層のパーセプトロンは線形領域だけしか表現できないのに対して、多層のパーセプトロンは非線形領域を表現することができる。
- 多層のパーセプトロンは、(理論上)コンピュータを表現できる。
3. ニューラルネットワークを動かす
パーセプトロンからニューラルネットワークへ
- データが有れば自動で重みを決めれる(=学習させる)→これを機械学習という
ニューラルネットワーク
- ニューラルネットワーク=入力信号の総和
- y=h(b+w1x1+w2x2)
- h(x)は活性化関数(activation function)という
- 入力層は層として数えないので、入力層・中間層(隠れ層)・出力層で構成されている場合は「2層のニューラルネットワーク」といえる。
- パーセプトロンは「入力値に重みをかけて、バイアスを足して0より大きいか否かで出力が0か1になるもの」だった
活性化関数
def step_function(x):
# xに対して一気(broadcast)に0より大きいか小さいかを評価
y = x > 0
# yをintにキャストしている
return y.astype(np.int)
step_function(np.array[-15, -10, 0.1, 10, 50])
array([ 0, 0, 1, 1, 1])
シグモイド関数
- ニューラルネットワークで扱うときはシグモイド関数にする
- Pythonのexpじゃなくて、NumPyのexpを使うことが肝
- 「Pythonでfor文かいたら負け*1」
- なめらかな数値に変えることができるので、値を連続的に扱える(微分可能)
- ステップ関数もシグモイド関数、両方どちらとも非線形関数なのがポイント
- パーセプトロンのできることしかできていない
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.array([-1, 1, 2])
array([ 0.26894142, 0.73105858, 0.88079708])
多次元配列
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.array([[1, 2], [3, 4], [5, 6]]) np.dot(A,B)
array([[22, 28], [49, 64]])
3層ニューラルネットワークの実装
読み方
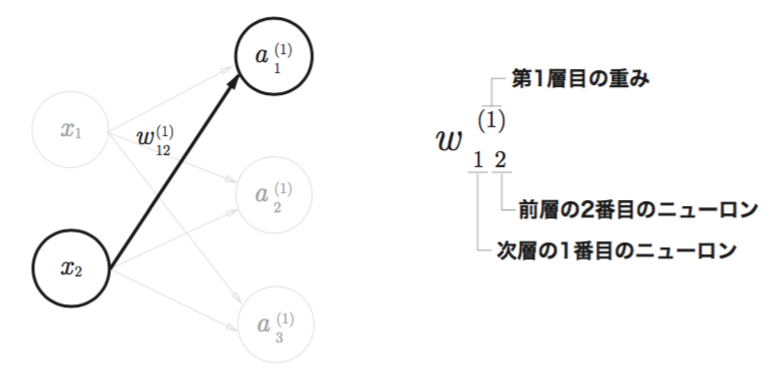
実装

- 最終的なゴールは入力層(x1, x2,…)から出力層(y1, y2,…)が導かれるものにしたい
(a1(1), a2(1), a3(1)) =
- a1(1) = w11(1)x1+w12(1)x2+b1(1)
- a2(1) = w21(1)x1+w22(1)x2+b2(1)
- a3(1) = w31(1)x1+w32(1)x2+b3(1)
最後の活性化関数(最後の中間層から出力層への信号の伝達)だけがidentity_function関数(恒等関数)を利用する
実装まとめ
こんな感じになる(networkで定められている値は決め打ち)
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [ 0.31682708 0.69627909]
出力層の設計
- 恒等関数→回帰問題に使う(連続した値を予想するとか、人物の写真から体重を予測するとか)
- ソフトマックス関数→分類問題に使う(あるデータの集まりをクラス(まとまり)に分ける。数字画像の認識0から9の画像を認識させると、その画像に写っている数字が何なのかを認識して計算してくれるとか)
ソフトマックス関数の実装上の注意
- 指数関数exp()が分母と分子に存在するので、floatの範囲を超えて結果が不安定になりがち
- 定数として入力信号の最大値max(a1, …, an)を引いておく
- 「指数関数の引数に定数を足しても引いても値は変わらない」という指数関数の特性を利用している
- 必ず分母のほうが多いので値が絶対に0から1.0の間の実数になり、出力の総和は1になる。
- なので、ソフトマックス関数の出力は「確率」として解釈ができる
- ※ソフトマックス関数を適用しても各要素の大小関係は変わらないので、分類問題を解く際には適用を省略できる
出力層のニューロンの数
- 分類問題では分類したいクラスの数に設定するのが普通
- ある入力画像が数字の0から9のどれかを予測したい時には出力層のニューロンは10個に設定する
手書き数字認識
バッチ処理
- ニューラルネットワークの計算効率を上げるには一挙に100個とか判定した方がいいので、入力値を100個にまとめて計算するとかやる
- もちろん100個ごとじゃなくて全部まるごとでも大丈夫。
まとめ
- ニューラルネットワークでは、活性化関数としてシグモイド関数や ReLU 関数のような滑らかに変化する関数を利用する。
- NumPy の多次元配列をうまく使うことで、ニューラルネットワークを効率良く実装することができる。
- 機械学習の問題は、回帰問題と分類問題に大別できる。
- 出力層で使用する活性化関数は、回帰問題では恒等関数、分類問題ではソフトマックス関数を一般的に利用する。
- 分類問題では、出力層のニューロンの数を分類するクラス数に設定する。
- 入力データのまとまりをバッチと言い、バッチ単位で推論処理を行うことで、計算を高速に行うことができる。
感想
- ニューラルネットワーク学生のときにやったなー懐かしい。思い出そう。
- おもったより難しくなさそう。Jupyterでとりあえずゴリゴリやれば面白そう。
- コンピュータじゃないかのチェックで英数字の判定させてるところ、そろそろつらいな。
- 自分の好きなアイドルとかでDeep Learningさせたくなるの分かる。
*1:ほんまか工藤案件。